Cómo calcular la velocidad de escape

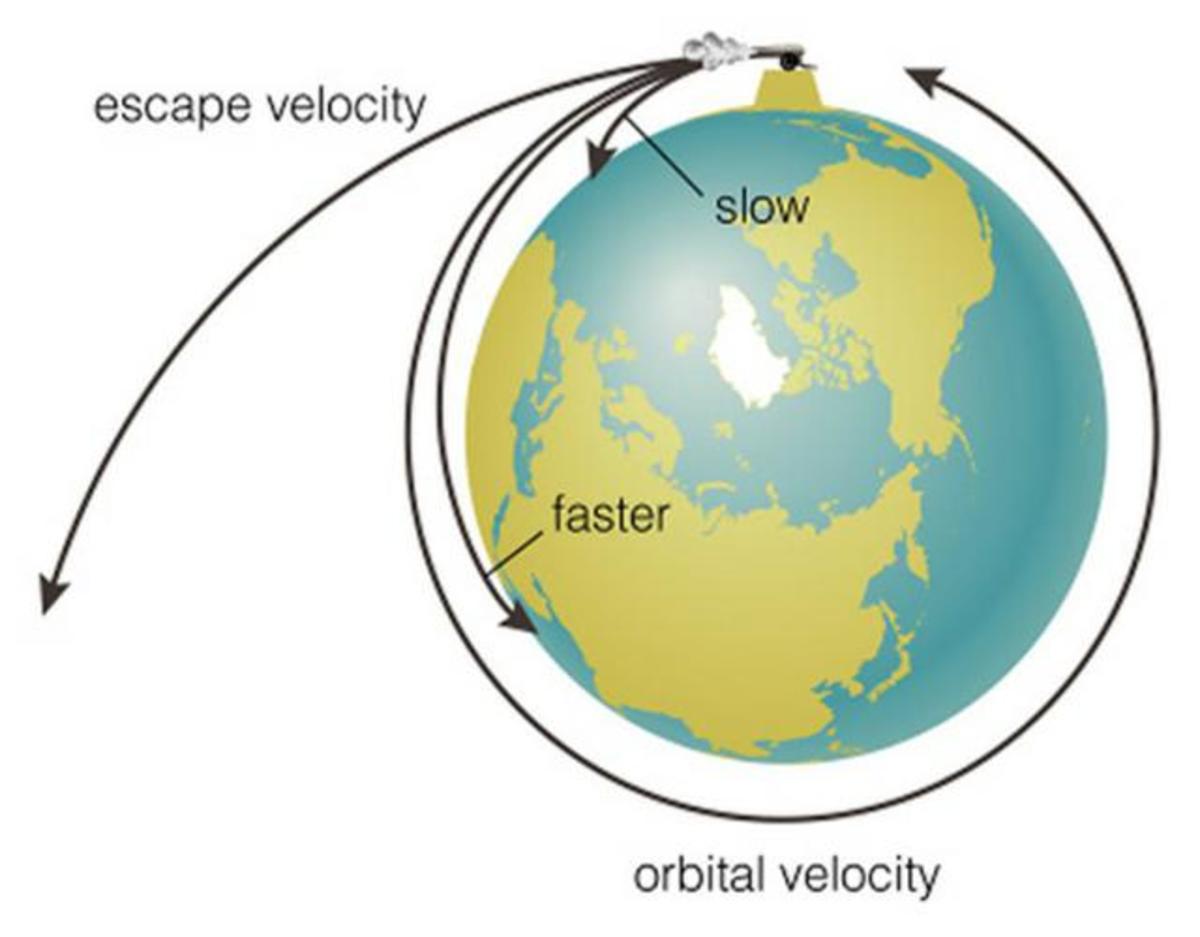
La velocidad de escape es la velocidad necesaria para que un móvil venza la fuerza gravitacional que lo atrae al planeta en el que se encuentra. En este QueHowTo te enseñamos cómo calcular la velocidad de escape. Sigue leyendo si quieres saber más.

Calcular la velocidad de escape paso a paso

1. Definimos la ecuación para obtener la velocidad de escape.
   • v={\sqrt {{\frac {2GM}{r}}}}
   • En esta ecuación se asume que el planeta en el que estás es completamente esférico y tiene una densidad constante. Sin embargo, en realidad la velocidad de escape depende de tu localización geográfica en la superficie porque el planeta se abulta en el ecuador y tiene una densidad ligeramente variable debido a su composición.
2. Entendiendo las variables de la ecuación.
   • G=6.67\times 10^{{-11}}{{\rm {\ N\ m^{{2}}\ kg^{{-2}}}}} es la constante gravitacional de Newton. El valor de esta constante nos da idea de que la gravedad es en realidad una fuerza bastante débil. Fue obtenida experimentalmente por Henry Cavendish en 1798, pero se ha comprobado que es considerablemente complicado medirla con precisión.
     • G puede ser expresado en unidades fundamentales6.67\times 10^{{-11}}{{\rm {\ m^{3}\ kg^{{-1}}\ s^{{-2}}}}}, dado que 1{{\rm {\ N}}}=1{{\rm {\ kg\ m\ s^{{-2}}}}}.
   • La masa M y el radio r dependen directamente del planeta del que deseas salir.
   • Debes convertir las unidades al SI. Esto es, la masa debe ser expresada en kilogramos (kg) y la distancia en metros (m). Si tienes variables en diferentes unidades, como millas, debes hacer la conversión al SI.
3. Determina la masa y el radio del planeta en el que estás. Para la Tierra, asumiendo que estás a nivel del mar, r=6.38\times 10^{{6}}{{\rm {\ m}}} y M=5.98\times 10^{{24}}{{\rm {\ kg}}}.
   • Para otros planetas y lunas, puedes buscar tablas con los datos de masa y radio.
4. Sustituye los valores en la ecuación. Ahora que ya tienes la información necesaria, puedes comenzar a resolver la ecuación.
   • v={\sqrt {{\frac {2(6.67\times 10^{{-11}}{{\rm {\ m^{{3}}\ kg^{{-1}}\ s^{{-2}}}}})(5.98\times 10^{{24}}{{\rm {\ kg}}})}{(6.38\times 10^{{6}}{{\rm {\ m}}})}}}}
5. Análisis dimensional. Recuerda que debes estar pendiente de las unidades que manejas, para poder cancelarlas conforme a las operaciones que realizas, para obtener una respuesta dimensionalmente consistente.
   • {\begin{aligned}v&={\sqrt {{\frac {2(6.67)(5.98)}{(6.38)}}\times 10^{{7}}{{\rm {\ m^{{2}}\ s^{{-2}}}}}}}\\&\approx 11200{{\rm {\ m\ s^{{-1}}}}}\\&=11.2{{\rm {\ km\ s^{{-1}}}}}\end{aligned}}
   • En el último paso, convertimos la respuesta de unidades de SI a {{\rm {\ km\ s^{{-1}}}}} multiplicando por el factor de conversión {\frac {{\text{1 km}}}{{\text{1000 m}}}}.

Sabemos que te puede costar en un principio pero te vamos a dejar un vídeo para que lo entiendas mejor. Aquí te dejamos el vídeo:

---