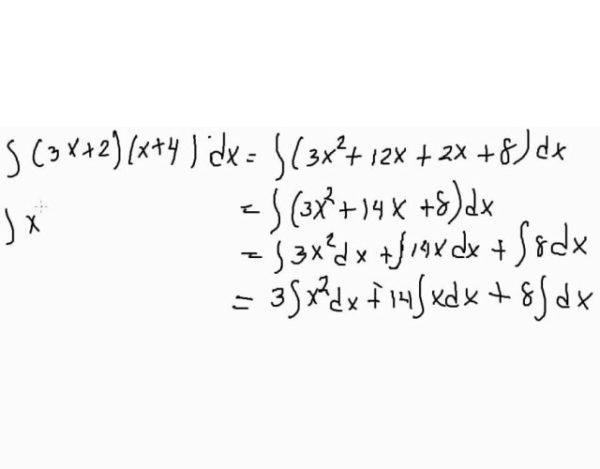Resolver integrales es sumamente sencillo, siempre y cuando se realicen los pasos como deben ser. Ahora bien, te indicaremos la manera correcta a seguir.
Se trata de la operación inversa a la derivación. Existen algunas funciones cuyas integrales pueden evaluarse mediante las técnicas estándar que se mencionan en este artículo, pero, para muchas más de ellas, esto no es así.
Tan sencillo y práctico como intentar sumar y restar raíces cuadradas.
Pasos para resolver integrales
- Evalúa la integral de una función par. En todos los casos, las funciones pares son simétricas alrededor del Eje Y.
La integral será 0 cuando los límites sean simétricos.
- Por consiguiente, evalúa la integral de una función impar. Asimismo, las funciones impares son simétricas alrededor de su origen (imagina que giras 180 grados la parte negativa de la función). De esta forma, esto hará que quede por encima de la parte positiva.
La manera correcta por sustitución
- En primer lugar, hay que buscar la línea. Se trata de una técnica de cambio de variables. Como se verá más adelante, esta constituye la versión análoga de la regla de la cadena para las derivadas.
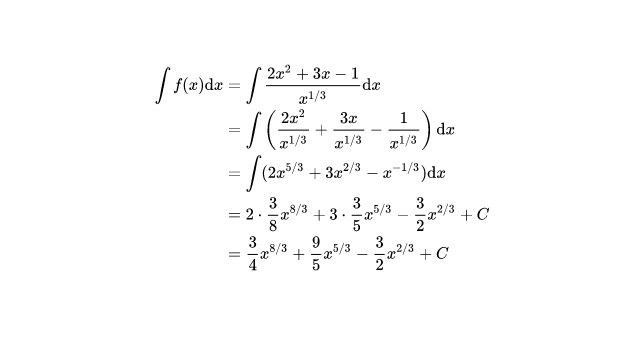
Se tiene que seguir al detalle cada uno de los pasos mismos.
- Posteriormente, hay que analizar la integral de X.
- Luego, evalúa y reescribe la integral en términos de la variable original. En el caso de las integrales indefinidas, deberás reescribirlas en términos de la variable original.
- Evalúa la siguiente integral con los límites dados. Asimismo, observarás que este es un caso de integración por sustitución en el que es necesario «sustituir hacia atrás«.
- Debes asegurarte de cambiar también los límites según la sustitución.
- Encuentra el valor de X y sustituye. A esto se refería la sustitución hacia atrás mencionada anteriormente.
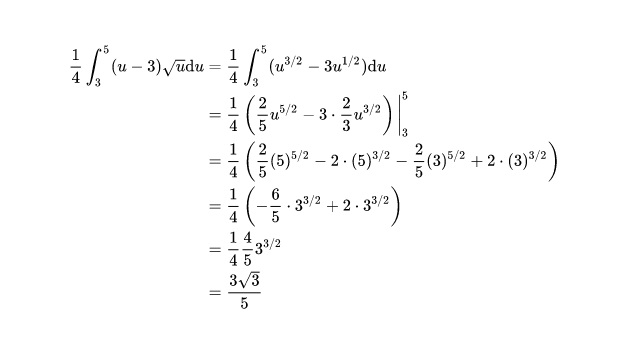
Prosigue al detalle cada uno de los pasos.
- Expande y evalúa. Una de las ventajas de las integrales definidas es que, antes de evaluar, no tienes que reescribir la antiderivada en términos de la variable original.
Resolver integrales en partes
- Primeramente, hay que ubicar en línea para aprender cómo realizar la integración por partes. Este método tiene el principal objetivo de integrar el producto de dos funciones. Mediante esta técnica, se simplifica la integral hasta obtener una que con suerte será más fácil de evaluar.
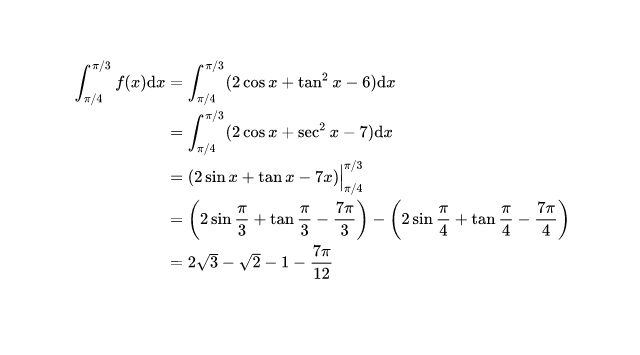
Una vez dado cada uno de los pasos, podrás decantar en increíbles resultados.
- Analiza la integral de la función logarítmica. Esta resulta ser una aplicación simple de la integración por partes.
- Elige un los valores y produce el reordenamiento. De esa forma, la evaluación quedará trivial.
Ante todo lo indicado, dejaremos las herramientas y demás consejos a tener en cuenta para poder lograr los objetivos. Ahora bien, te indicaremos la manera a perseguir como tiene que ser: