Los radicales es una parte de las matemáticas que no debemos olvidar. Puede resultar difícil pero cuando le pillas el truco no puedes parar. En este QueHowTo te enseñamos cómo multiplicar radicales. Sigue leyendo si quieres saber más.
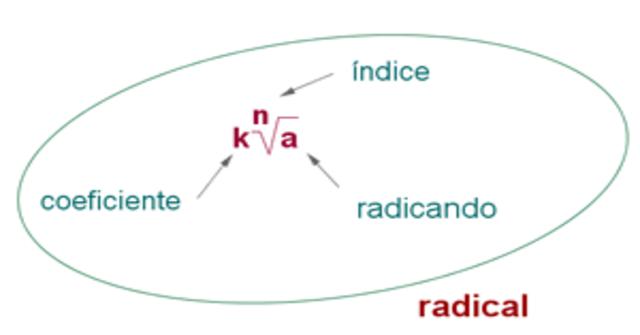
Cuando no puedes simplificar un número para quitar una raíz cuadrada (o una raíz cúbica, etc.) entonces es un radical. Ejemplo:
- √2 (la raíz cuadrada de 2) no se puede simplificar más así que es un radical. Pero √4 (la raíz cuadrada de 4) sí se puede simplificar (queda 2), así que no es un radical.
Multiplicar radicales: Paso a paso
- Asegúrate de que los radicales tengan el mismo índice. Para multiplicar radicales utilizando el método básico, deberán tener el mismo índice. El «índice» es el número pequeño que se encuentra justo a la izquierda de la línea superior en el símbolo del radical. Si no hay ningún número, se entiende que es una raíz cuadrada (índice 2) y se puede multiplicar por otras raíces cuadradas. Puedes multiplicar radicales con diferentes índices también.
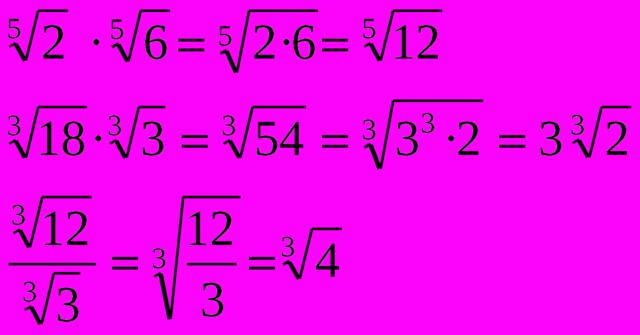
- Multiplica los números que están debajo del radical. Tan solo multiplica los números debajo del símbolo de radical y deja el resultado ahí adentro.
- Simplifica tus radicales. Después de multiplicar radicales, es muy probable que puedas simplificarlos a cuadrados perfectos o cubos perfectos, o que puedas simplificarlos encontrando un cuadrado perfecto como factor del producto final.
Ejemplos de como realizarlo
Ejemplo. 1: √(18) x √(2) = ? -> √(18) x √(2) = √(36) -> √(36) = 6. 36 es un cuadrado perfecto porque es el resultado de 6×6. La raíz cuadrada de 36 es simplemente 6.
Ejemplo 2: √(10) x √(5) = ? -> √(10) x √(5) = √(50) -> √(50) = √(25 x 2) = √([5 x 5] x 2) = 5√(2). Aunque 50 no es un cuadrado perfecto, 25 es un factor de 50 (porque divide el número de manera exacta) y es un cuadrado perfecto. Puedes convertir 25 en 5×5 (sus factores), y sacar uno de los 5s de la raíz para simplificar la expresión.
Ejemplo 3: 3√(3) x 3√(9) = ? -> 3√(3) x 3√(9) = 3√(27) -> 3√(27) = 3. 27 es un cubo perfecto porque es el producto de 3 x 3 x 3. La raíz cúbica de 27 es 3.
Consejos
- Los signos radicales son otra manera de expresar los exponentes fraccionales. En otras palabras, la raíz cuadrada de un número puede también expresarse como dicho número elevado a la potencia ½, la raíz cúbica de un número es igual a la potencia 1/3 de dicho número, etc.
- Si se separa un «coeficiente» del signo de radical por un signo de más o de menos, en realidad no se trata de un coeficiente; se trata de un término independiente que debe manejarse por separado. Si un radical y otro término se encuentran dentro de los mismo paréntesis (por ejemplo, (2 + (raíz cuadrada)5), deberás trabajar con 2 y con (raíz cuadrada)5 por separado al llevar a cabo tus operaciones dentro de los paréntesis, pero al trabajar fuera de los paréntesis deberás trabajar con (2 + (raíz cuadrada)5) en conjunto.
Te dejamos un vídeo sobre el tema: