Calcular derivadas es sumamente sencillo, siempre y cuando prosigas con los pasos mismos para una resolución adecuada. Ahora bien, aquí tendrás a mano la manera que deberás seguir.
Se trata de un operador que encuentra la razón de cambio instantánea de una cantidad. Se pueden usar las derivadas para obtener características útiles sobre una función.
Tan sencillo y práctico como calcular la velocidad instantánea.
Pasos para calcular derivadas
- En primer lugar, es fundamental comprender el concepto de la derivada. Para encontrar la pendiente de la función, se toman dos puntos en la línea y se ingresan sus coordenadas en la relación. Por supuesto que esto puede usarse únicamente con gráficos lineales.
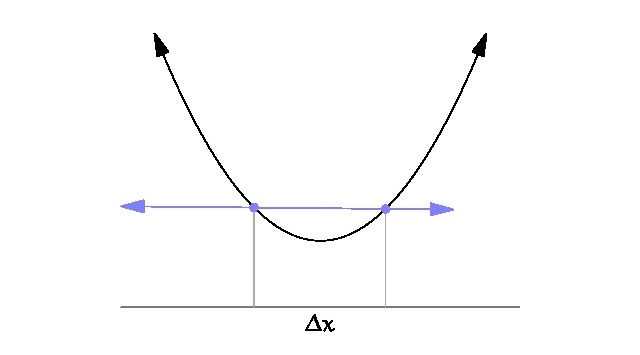
En el caso de las funciones no lineales, la línea será curva y, por tanto, si obtienes la diferencia entre dos puntos, esto solo puede darte la razón de cambio promedio entre ellos.
- Luego, comprende la notación derivativa. Son dos las notaciones comunes para las derivadas, aunque también hay otras. Asimismo, reemplaza la función en el límite. Y evalúa el límite.
- Por consiguiente, emplea la regla de la potencia cuando sea una función polinómica de grado n. Multiplica el exponente por el coeficiente y réstale 1 a la potencia.

Obviamente, la regla de la potencia facilita mucho más encontrar derivadas de polinomios.
- Después, vuelve a diferenciar. Obtener una derivada de mayor orden de una función simplemente quiere decir que obtienes la derivada de la derivada. Obtén la tercera derivada del ejemplo anterior.
- Posteriormente, busca en línea para obtener una explicación completa de la regla del producto. Emplea la regla del cociente para obtener derivadas de funciones racionales.
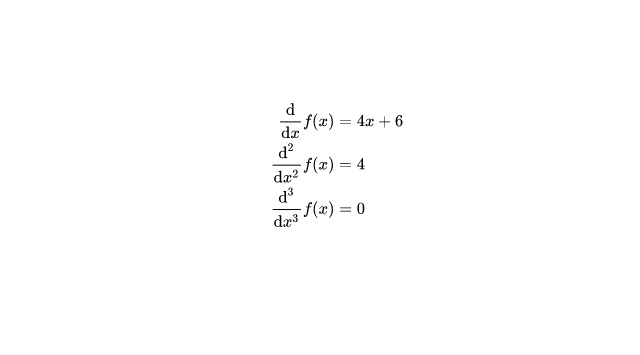
Como ocurre con los productos en general, la derivada de un cociente no equivale al cociente de las derivadas.
- A continuación, emplea la regla de la cadena para las funciones que estén una dentro de otra. Observa que esta función puede dividirse en dos funciones elementales. Luego, queremos encontrar la derivada de la composición.
- Por último, resulta muy aconsejable memorizarse derivadas trigonométricas básicas y cómo derivarlas.
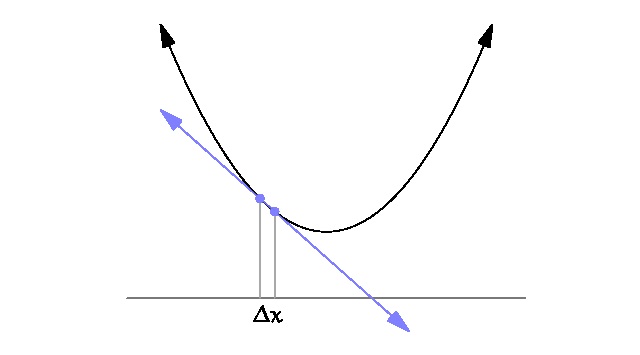
Hay que estar al pie de cada detalle, para poder siempre tenerle una solución a cada índice.
Ante todo lo indicado, te dejamos un vídeo explicativo, para poder proseguir con referencias y demás conocimientos mismos. Ahora bien, vamos a pasar al contenido audiovisual:

