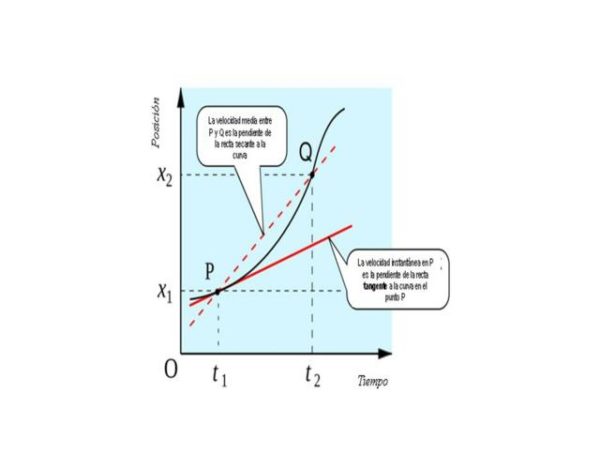
La velocidad se define como la velocidad que tiene un objeto en una dirección dada. En este QueHowTo te enseñamos cómo calcular la velocidad instantánea. Sigue leyendo si quieres saber más sobre este tema.
En muchas situaciones comunes, para hallar la velocidad debemos utilizar la ecuación v = s/t, donde “v” es la velocidad, “s” es el desplazamiento desde la posición inicial del objeto y “t” es igual al tiempo transcurrido. Sin embargo, técnicamente esto solo da la velocidad promedio del objeto durante su recorrido. Mediante el cálculo, es posible determinar la velocidad de un objeto en cualquier momento durante su recorrido. Esto se conoce como velocidad instantánea y se define con la ecuación v = (ds)/(dt) o, en otras palabras, la derivada de la ecuación de la velocidad promedio del objeto.
Calcular la velocidad instantánea, paso a paso
- Comienza con una ecuación para la velocidad en términos de desplazamiento. Para hallar la velocidad instantánea de un objeto, primero debemos tener una ecuación que nos diga su posición (en términos de desplazamiento) en un determinado punto en el tiempo. Esto significa que la ecuación debe tener la variable s en un lado aislada y t en el otro (no necesariamente aislada), de esta manera:
s = -1.5t2 + 10t + 4
- Toma la derivada de la ecuación. Para hallar la derivada de la fórmula de desplazamiento, diferencia la función con esta regla general para hallar las derivadas: Si y = a*xn, Derivada = a*n*xn-1. Esta regla se aplica a todos los términos en el lado “t” de la ecuación.
- Reemplaza la “s” con “ds/dt”. Para demostrar que nuestra ecuación nueva es una derivada de la primera, reemplazaremos “s” con la notación “ds/dt”. Técnicamente, esta notación significa “la derivada de s con respecto a “t”. Una forma más sencilla de pensar en esto es simplemente considerar que ds/dt es la pendiente de cualquier punto determinado en la primera ecuación. Por ejemplo, para hallar la pendiente de la línea hecha por s = -1.5t2 + 10t + 4 en t = 5, simplemente le daremos un valor de “5” a “t” en su derivada.
- Dale un valor a “t” para la nueva ecuación a fin de hallar la velocidad instantánea. Ahora que tienes la ecuación derivada, hallar la velocidad instantánea en cualquier punto del tiempo. Por ejemplo, si queremos hallar la velocidad instantánea en t = 5, simplemente reemplazaríamos “5” por “t” en la derivada ds/dt = -3 + 10. Luego, resolveremos la ecuación de la siguiente manera:
ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 metros por segundo
Te dejamos un vídeo sobre el tema: